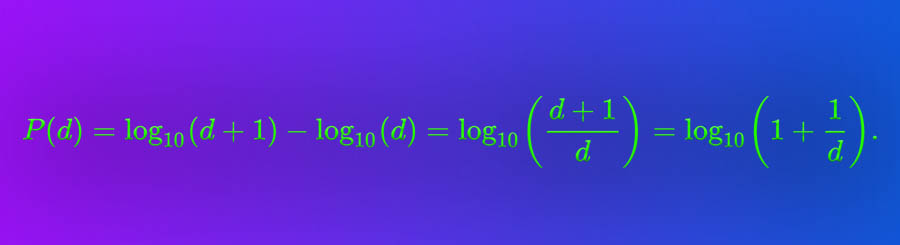Entenda como aplicar a Lei de Benford
A lei de Benford basicamente explica que se você escolher um número aleatório a probabilidade desse número possuir o 1 como primeiro algoritmo é maior que 2 que é maior que 3 e assim por diante; não é atoa que essa lei também é conhecida como a lei do primeiro dígito.
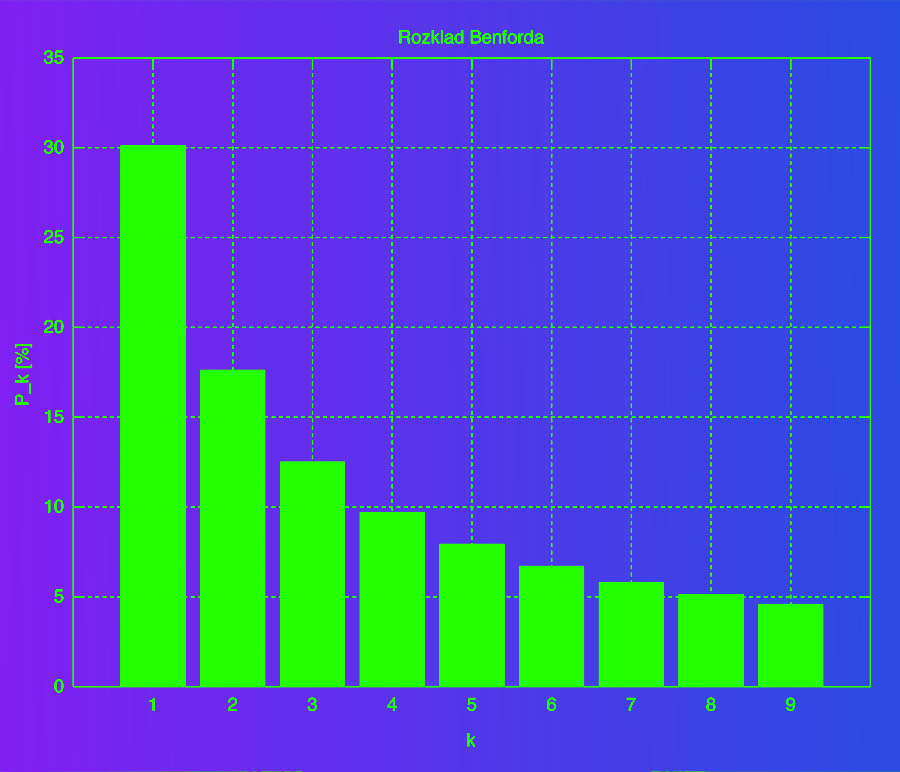
Se nós observarmos um gráfico desta lei vamos notar que a porcentagem de cada número aparecer é cada vez menor; o número 1 tem a probabilidade de 30,1% o número 2 já diminui para 17, 6% sendo assim quando chegarmos no número 9 a probabilidade é mínima.
Mas não pense que ela foi algo citado a pouco tempo, sua primeira citação matemática foi em 1938, pelo físico Benford, mas antes dele falar sobre essa lei Simon Newcomb já havia citado a existência dela, entretanto quem a comprovou foi Benford.
Agora você deve estar se perguntando, e isso se encaixa no meu dia a dia? Pra que serve essa lei?, bem…Essa lei se encaixa em tudo, desde um placar de jogo até uma eleição para presidente do seu país.
Vamos falar um pouco sobre o que motivou a descoberta desta lei; Por volta de 1881 o astrônomo Simon Newcomb fez as primeiras observações. Ele notou que as primeiras páginas de um livro de Logaritmos era mais gasta que as páginas do meio e fim, sendo assim elas eram mais usadas. Essa pesquisa o levou a pensar que em uma lista de um conjunto aleatório de números os números que começam com o dígito 1 são mais numerosos do que os que começam com 2,3 e assim sucessivamente. Depois disso o fenômeno foi deixado de lado por uns tempos até que, em 1938 Frank Benford redescobriu a lei, Benford coletou vários números com mais de 20 dezenas diferentes; dentre eles tinham mais de 300 superfícies de rios, tamanhos de locais de 3259 lugares nos Estados Unidos, 1.800 pesos moleculares, entre muitos outros. A quantidade de números usados ultrapassou 20.000, entretanto, só em 1995 o matemático Theodore P. Hill conseguiu provar o fenômeno por trás dessas distribuições.
A lei: Como dito por Newcomb, o primeiro dígito de uma lista numérica segue uma distribuição logarítmica. O modelo teórico foi mostrado por benford onde a probabilidade do dígito d é explicada pelo logaritmo: